
Reflection of a point (a, b) about the straight line x=y results in the new point having coordinates (b, a). f (x) (x) g (x) (- x) Reflection on x-axis Take any function f (x) and it to - f (x), the graph of - f (x) will be the graph of f (x) reflected on the x axis. It can be reflected about any line, even a slant line, called the axis of reflection. Take any function f (x) and change x to - x, the graph of f (- x) will be the graph of f (x) reflected on the y axis. Figure 1 shows the graph of f(x) along with the graphs of the functions reflected about the x and y axis.Ī function need not be reflected only about the coordinate axes. This is a different form of the transformation. Reflection of a point about the y axis results in a new point whose y coordinate is the same as the original point, but the x coordinate has an opposite sign. In a reflection about the x-axis, the x-coordinates stay the same while the y-coordinates take on their opposite signs. Since the line of reflection is no longer the x-axis or the y-axis, we cannot simply negate the x- or y-values. Here are the graphs of y f ( x ) and y - f ( x ). Making the output negative reflects the graph over the x -axis, or the line y 0. z=f(-x) then the graph of the new function will be a reflection of the graph of the original function about the y-axis. We can also reflect the graph of a function over the x-axis (y 0), the y-axis(x 0), or the line y x. Similarly, if we change the sign of x in the function, i.e. When a point is reflected about the x axis, the x coordinate remains the same, but the y coordinate changes sign.
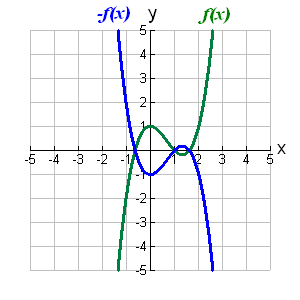
It looks as if a mirror has been placed exactly on the x-axis, which is reflecting the original graph. the sign of the entire function as z=-y=-f(x), then the graph of this new function will be a reflection of the graph of the original function about the x-axis.
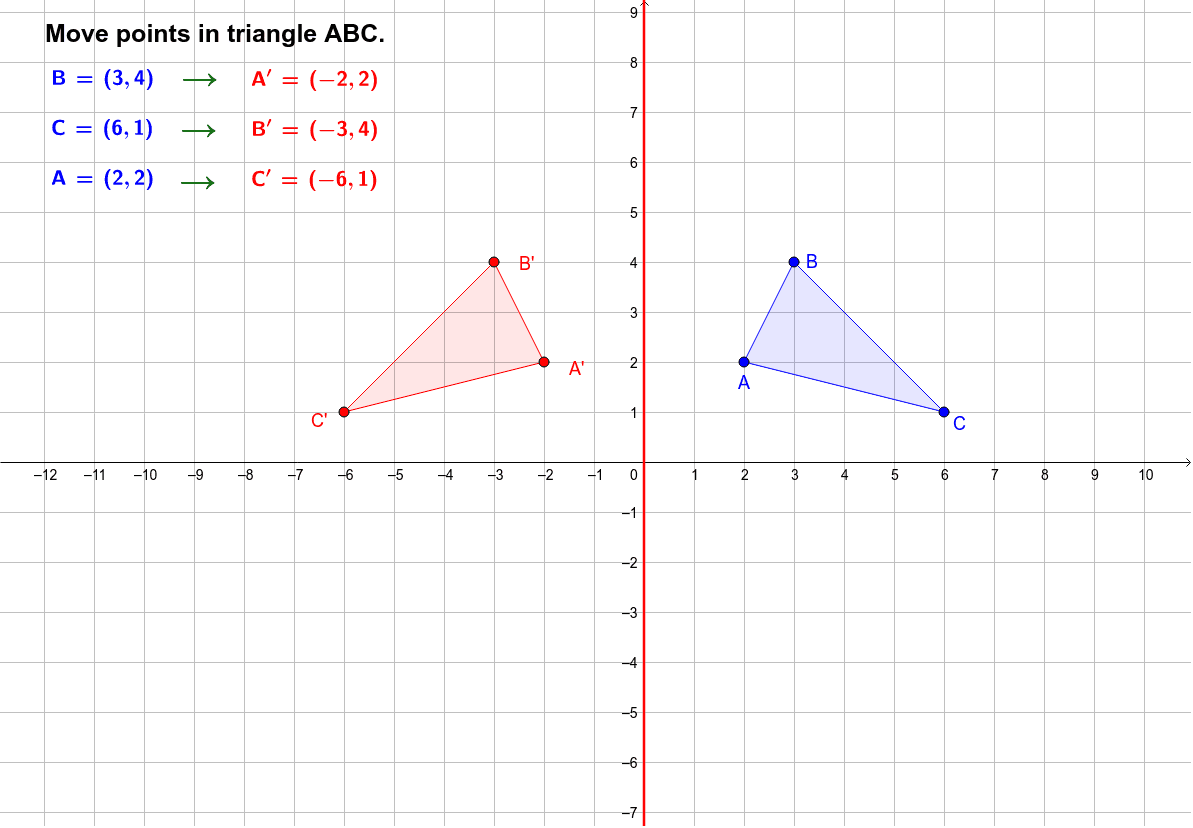
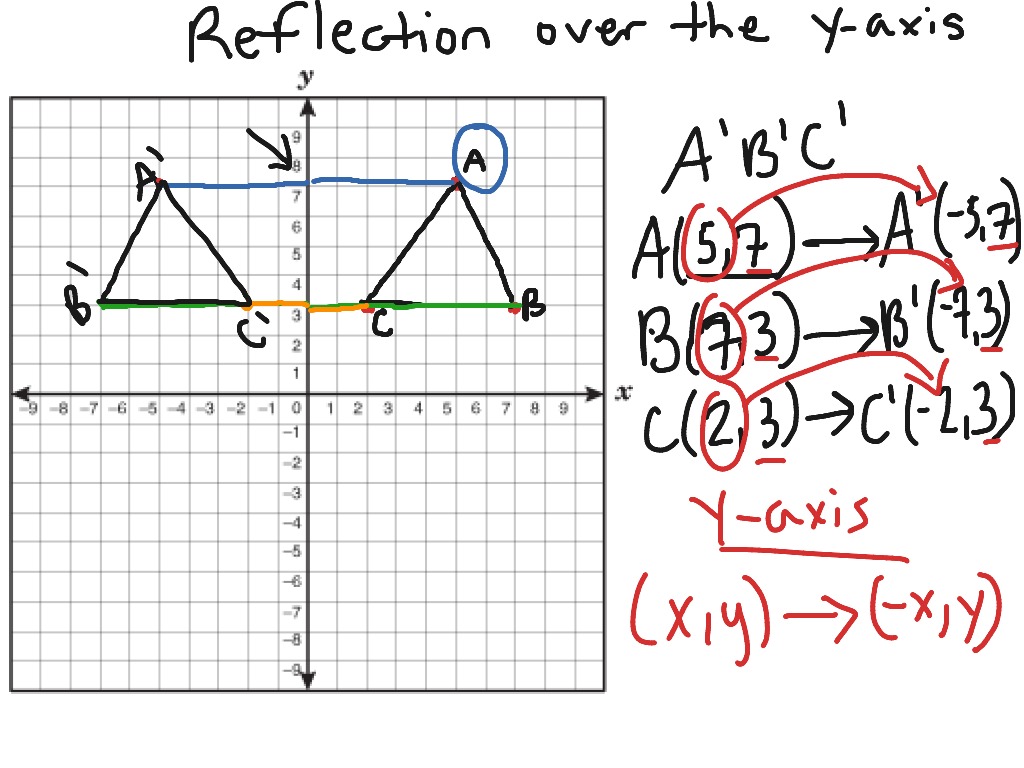
A vertical reflection reflects a graph vertically across the. Images/mathematical drawings are created with GeoGebra.Consider a function, y=f(x). Another transformation that can be applied to a function is a reflection over the x or y-axis. Read more Halfplane: Definition, Detailed Examples, and Meaning Let’s take a look at the two triangles plotted on the same $xy$-plane. y f (-x) The graph of y f (-x) can be obtained by reflecting the graph of. We normally label the image using the pre-image’s points but this time, we add a prime symbol to each of these points’ labels. reflection over x axis functionReflection over y axis equation - Math Scanner. Image: The reflected triangle and final version after reflecting the triangle over.Pre-image: The original image (for this discussion, the triangle) that we’re reflecting over a line.When studying and working on the reflection of polygons like the triangle, it’s important to know the following terms: Triangle reflection is the figure obtained when a triangle is flipped on a coordinate system based on a line of reflection. By the end of our discussion, we want you to feel confident when working on reflections of triangles.
REFLECTION ON Y AXIS FUNCTION HOW TO
By learning how to reflect these figures over a given line of reflection, we’ll apply our understanding of reflecting points over a coordinate plane. Figure 3-9: Vertical and horizontal reflections of a function. In this article, we’ll show you the process of reflecting a triangle on a coordinate plane. A vertical reflection reflects a graph vertically across the x -axis, while a horizontal reflection reflects a graph horizontally across the y -axis. The most common lines of reflection are the x-axis, the y-axis. Read more Triangle Proportionality Theorem – Explanation and Examples By examining the coordinates of the reflected image, you can determine the line of reflection.


 0 kommentar(er)
0 kommentar(er)
